넘어져도 다시 일어서는 오뚝이의 원리는
내부에 인위적인 무게추를 만들어
무게중심을 몰아주는 것으로 이루어지는데
어디로 넘어져도 단 하나의 자세로 고정되는 물체를
"하나의 안정평형점만을 가지는 다면체"
단안정다면체 라고 함
그런데 기하학의 숙제 중 하나는
오뚝이 처럼 인위적인 무게 추 없이
자체적인 단안정다면체를 찾는 것
힐베르트의 13번째 문제를 해결한
러시아의 대표적 수학자인 블라디미르 아놀드는
1995년 단일재료로 볼록한 단안정다면체가 존재하는가?
라는 질문을 던졌고
2006년, 헝가리의 수학자
가보르 도모코스가 Gömböc
라는 단안정다면체를 만들어내면서 이를 증명했고,
이 성과로 헝가리에서 훈장을 받게 됨
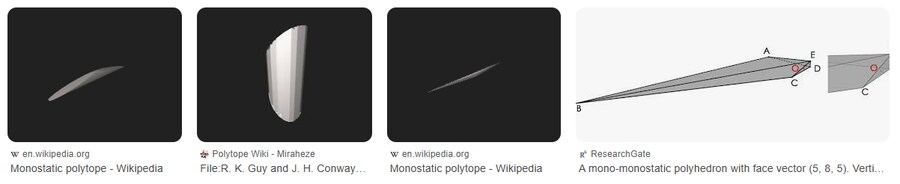
하지만 이 다면체는 둥근면이 존재했고
"일반적인 다면체 처럼 평평한 다면체도
다안정 다면체가 될 수 있을까?"
라는 의문에 들게 됨
그러던 2022년, 건축학과 학부생이었던 알마디는
"말은 많지 않지만 항상 생각에 잠겨있는 성실한 모습"
을 보이면서 도모코스 교수의 눈에 띄게 되고
사면체의 균형에 대한 개인과제를 받게 되는데
알마디는 무차별대입 알고리즘을 통해
"단안정 사면체" 를 구상했고
그 과정에서 결국 대학원을 가게 됨
그렇게 만들어진 이 사면체는
초정밀 엔지니어링 기업에 의뢰해
설계와 재료를 완벽하게 해결한 끝에
어떤 면으로 다면체를 두더라도
무조건 한면으로만 세워지는
단안정 사면체로 만들어짐
이 다면체를 만든 알마디는
"건축가가 되고 싶었는데
어쩌다 이렇게 된걸까요"
라는 소감을 남김







(IP보기클릭)211.245.***.***
(IP보기클릭)39.122.***.***
(IP보기클릭)121.140.***.***